Surplus production based catch-limit modifier

An MP that makes incremental adjustments to TAC recommendations based on the apparent trend in surplus production. Based on the theory of Mark Maunder (IATTC)

Usage

SPmod(x, Data, reps = 100, plot = FALSE, alp = c(0.8, 1.2), bet = c(0.8, 1.2))

Arguments

x: A position in the data object
Data: A data object
reps: The number of stochastic samples of the MP recommendation(s)
plot: Logical. Show the plot?
alp: Condition for modifying the TAC (bounds on change in abundance)
bet: Limits for how much the TAC can change among years

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

A numeric vector of TAC recommendations

Details

Note that this isn't exactly what Mark has previously suggested and is stochastic in this implementation.

The TAC is calculated as: $$\textrm{TAC}_y = \left\{\begin{array}{ll} C_{y-1} \textrm{bet}_1 & \textrm{if } r < \alpha_1 \\ C_{y-1} & \textrm{if } \alpha_1 < r < \alpha_2 \\ \textrm{bet}_2 (b_2 - b_1 + C_{y-2} ) & \textrm{if } r > \alpha_2 \\ \end{array}\right. $$ where $\textrm{bet}_1$ and $\textrm{bet}_2$ are elements in bet, $r$ is the ratio of the index in the most recent two years, $C_{y-1}$ is catch in the previous year, $b_1$ and $b_2$ are ratio of index in $y-2$ and $y-1$ over the estimate of catchability $\left(\frac{I}{A}\right)$, and $\alpha_1$, $\alpha_2$, and $\alpha_3$ are specified in argument alp.

Required Data

See Data-class for information on the Data object

SPmod: Cat, Ind

Rendered Equations

See Online Documentation for correctly rendered equations

References

http://www.iattc.org/Meetings/Meetings2014/MAYSAC/PDFs/SAC-05-10b-Management-Strategy-Evaluation.pdf

Author

T. Carruthers

Examples

SPmod(1, Data=MSEtool::Atlantic_mackerel, plot=TRUE)

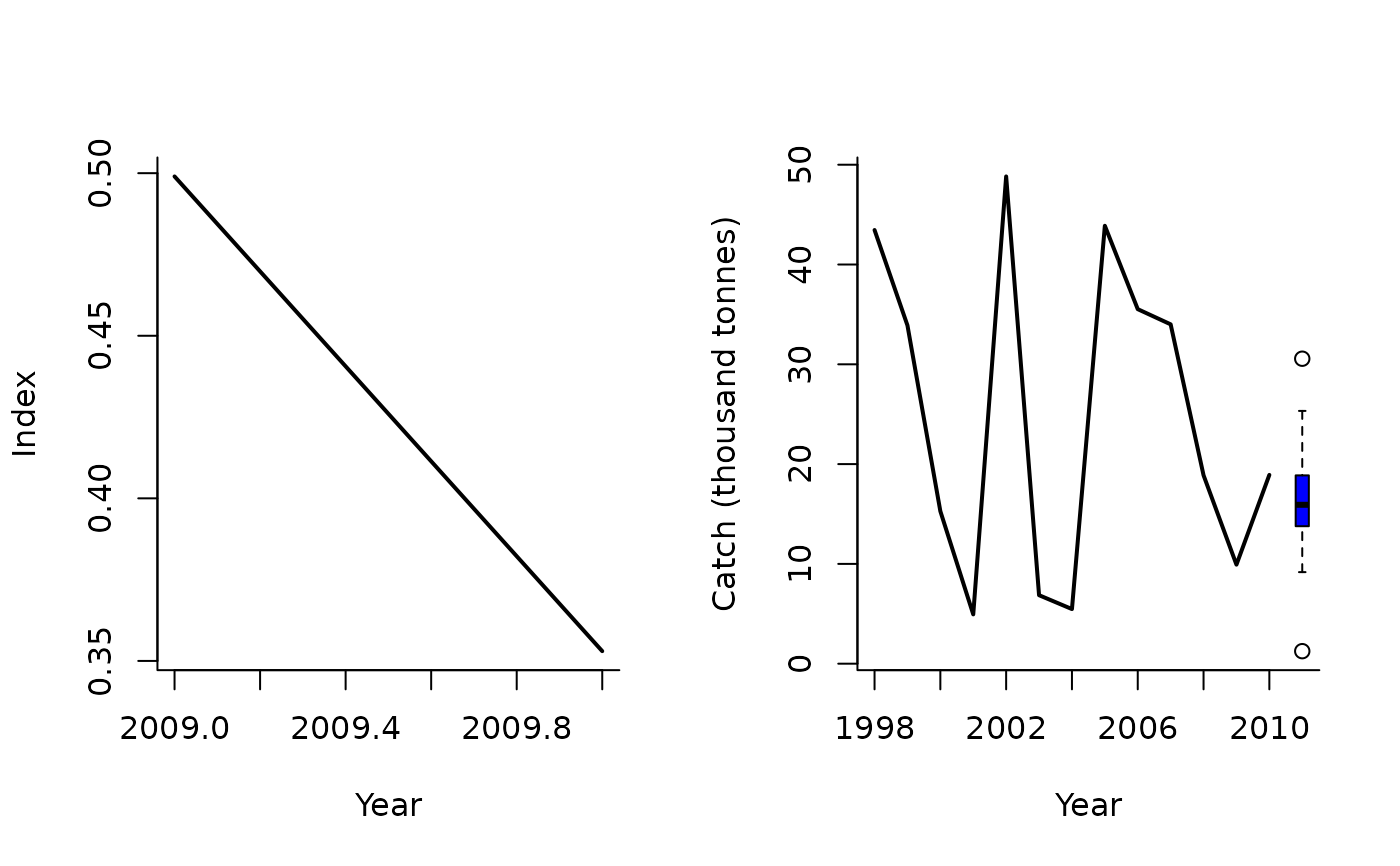#> TAC (median) 
#>     15.92228