Intrinsic rate of Increase MP

An MP proposed by Carl Walters that modifies the TAC according to trends in apparent surplus production that includes information from a demographically derived prior for intrinsic rate of increase

Usage

Rcontrol(
  x,
  Data,
  reps = 100,
  plot = FALSE,
  yrsmth = 10,
  gg = 2,
  glim = c(0.5, 2)
)

Rcontrol2(
  x,
  Data,
  reps = 100,
  plot = FALSE,
  yrsmth = 10,
  gg = 2,
  glim = c(0.5, 2)
)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

yrsmth

The number of years for smoothing catch and biomass data

gg

A gain parameters

glim

Limits for the change in TAC among years

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

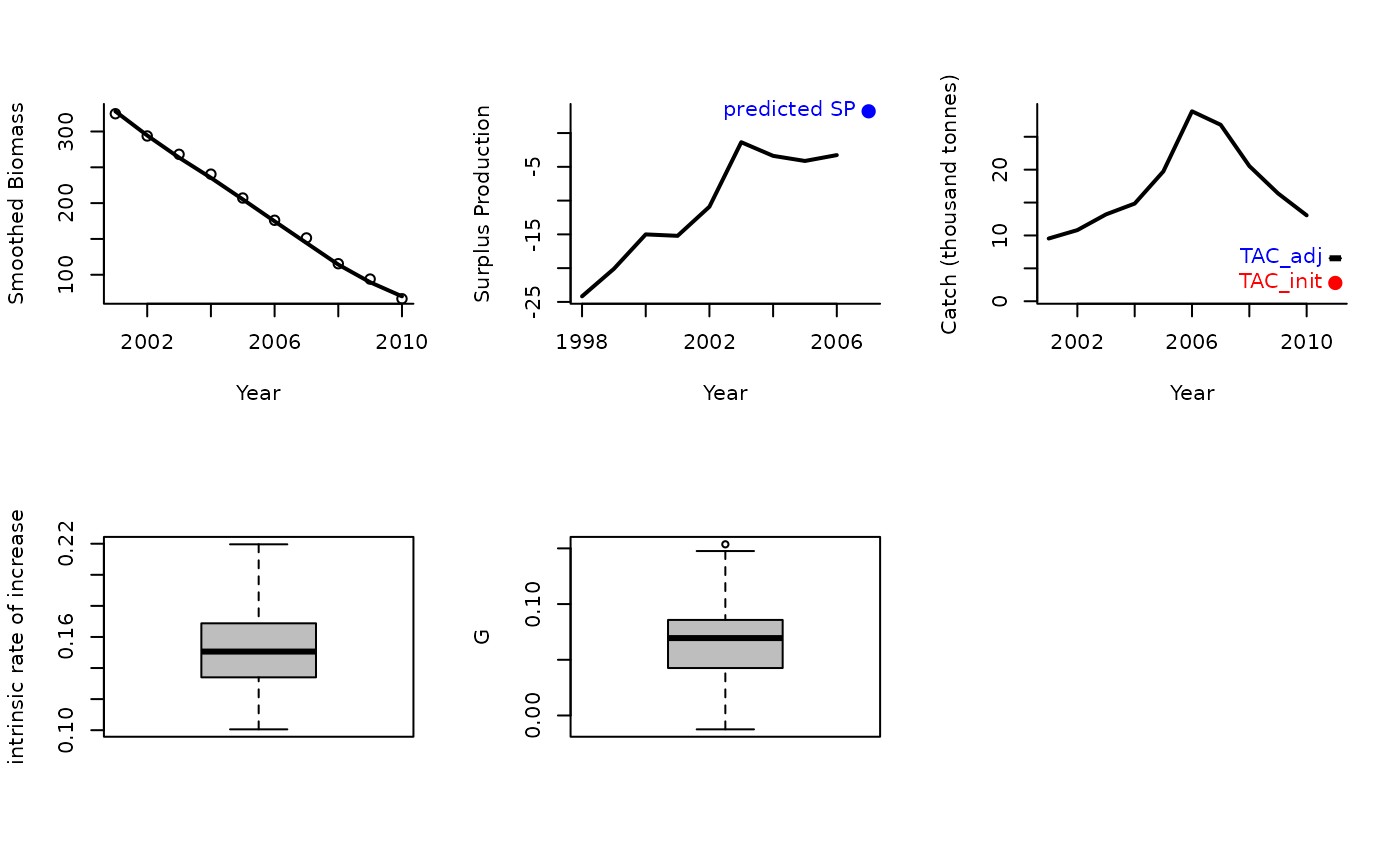
The TAC is calculated as: $$\textrm{TAC} = \textrm{SP} (1-gG)$$ where \(g\) is a gain parameter, \(\textrm{SP}\) is estimated surplus production, and \(G\) is: For Rcontrol: \(G = r (1-2D)\) where \(r\) is the estimated intrinsic rate of increase, and \(D\) is assumed depletion.

For Rcontrol2: \(G = r - 2bB_\textrm{hist}\) where \(B_\textrm{hist}\) is the smoothed biomass overlast yrsmth years and: $$b = \sum{\frac{\textrm{SP}}{B_\textrm{hist}} - r} \frac{\sum{B_\textrm{hist}}}{\sum{B_\textrm{hist}^2}} $$.

The TAC is subject to conditions limit the maximum change from the smoothed catch over the last yrsmth years by the glim argument, e.g, default values of glim = c(0.5, 2) means that maximum decrease in TAC is 50% of average catch and maximum increase is 2 x average catch.

Functions

• Rcontrol: Base version Rcontrol

• Rcontrol2: This is different from Rcontrol because it includes a quadratic approximation of recent trend in surplus production given biomass

Required Data

See Data-class for information on the Data object

Rcontrol: Abun, Cat, Dep, FMSY_M, Ind, L50, MaxAge, Mort, Year, steep, vbK, vbLinf, vbt0, wla, wlb

Rendered Equations

See Online Documentation for correctly rendered equations

References

Made-up for this package.

See also

Other Surplus production MPs: Fadapt(), SPMSY(), SPSRA(), SPmod(), SPslope()

Author

C. Walters and T. Carruthers

Examples

Rcontrol(1, Data=MSEtool::Atlantic_mackerel, plot=TRUE)

#> TAC (median) 
#>     6.529254 
Rcontrol2(1, Data=MSEtool::Atlantic_mackerel, plot=TRUE)

#> TAC (median) 
#>     6.529254