Itarget1 with an MPA

A example mixed control MP that uses the Itarget1 output control MP together with a spatial closure.

Usage

Itarget1_MPA(
  x,
  Data,
  reps = 100,
  plot = FALSE,
  yrsmth = 5,
  xx = 0,
  Imulti = 1.5
)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

yrsmth

Years over which to smooth recent estimates of surplus production

xx

Parameter controlling the fraction of mean catch to start using in first year

Imulti

Parameter controlling how much larger target CPUE / index is compared with recent levels.

Value

An object of class Rec-class with the TAC, Spatial slot(s) populated

Details

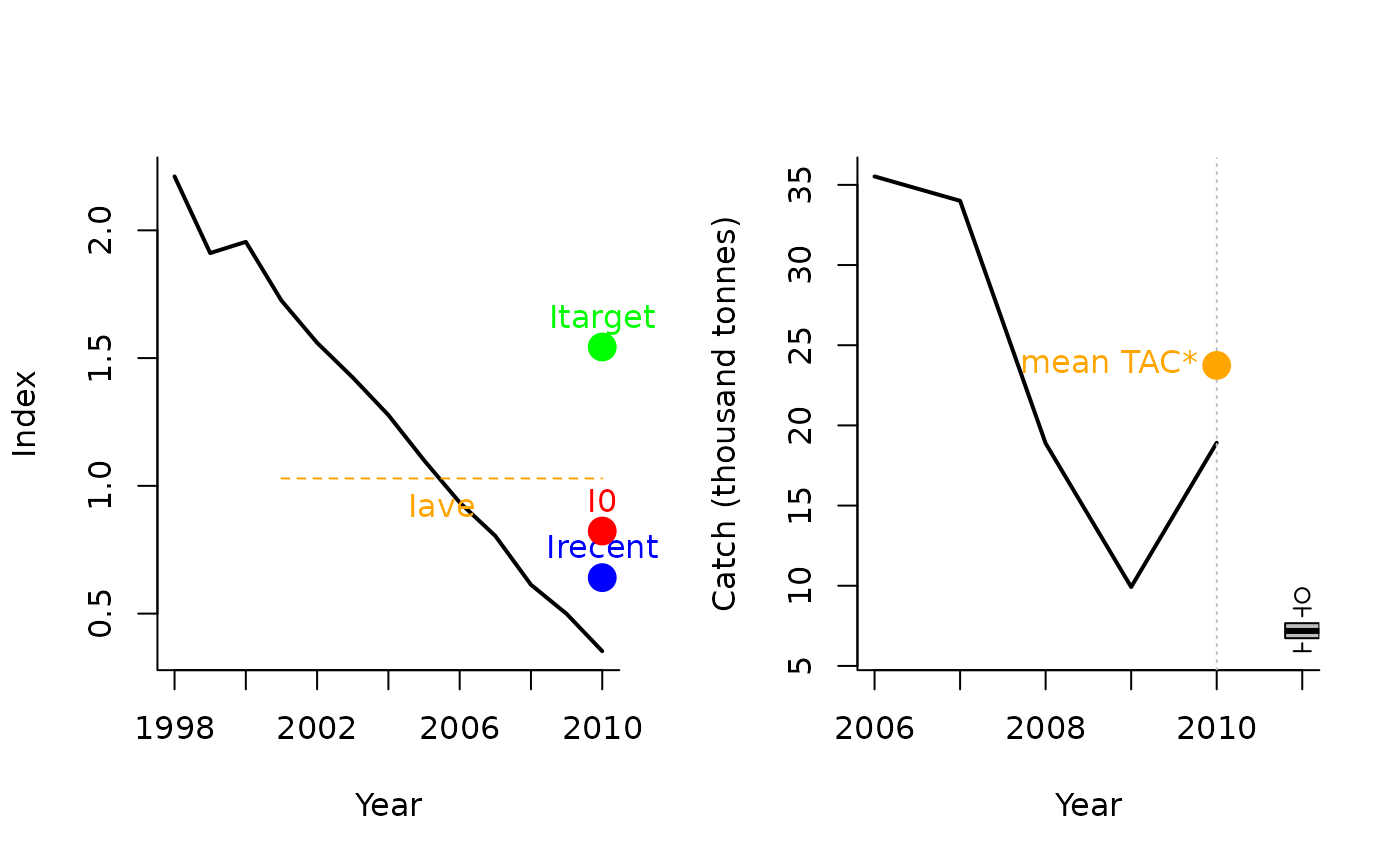
The TAC is calculated as: If \(I_\textrm{recent} \geq I_0\): $$\textrm{TAC}= 0.5 \textrm{TAC}^* \left[1+\left(\frac{I_\textrm{recent} - I_0}{I_\textrm{target} - I_0}\right)\right]$$

else: $$\textrm{TAC}= 0.5 \textrm{TAC}^* \left[\frac{I_\textrm{recent}}{I_0}^2\right]$$

where \(I_0\) is \(0.8 I_{\textrm{ave}}\) (the average index over the 2 x yrsmth years prior to the projection period), \(I_\textrm{recent}\) is the average index over the past yrsmth years, and \(I_\textrm{target}\) is Imulti times \(I_{\textrm{ave}}\), and \(\textrm{TAC}^*\) is: $$(1-x)C$$ where \(x\) is argument xx and C is the average catch over the last 5 years of the historical period.

This mixed control MP also closes Area 1 to fishing.

This MP has been included for demonstration purposes of a mixed control MP.

Required Data

See Data-class for information on the Data object

Itarget1_MPA: Cat, Ind, LHYear, Year

Rendered Equations

See Online Documentation for correctly rendered equations

See also

Other Index methods: GB_slope(), GB_target(), Gcontrol(), ICI(), Iratio(), Islope1(), Itarget1(), ItargetE1()

Examples

Itarget1_MPA(1, MSEtool::Atlantic_mackerel, plot=TRUE)

#> TAC (median)       Area 1       Area 2 
#>     7.180982     0.000000     1.000000