
Incremental Index Target MP
Itarget1.RdA management procedure that incrementally adjusts the TAC (starting from reference level that is a fraction of mean recent catches) to reach a target CPUE / relative abundance index
Usage
Itarget1(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0, Imulti = 1.5)
Itarget2(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0, Imulti = 2)
Itarget3(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0, Imulti = 2.5)
Itarget4(x, Data, reps = 100, plot = FALSE, yrsmth = 5, xx = 0.3, Imulti = 2.5)Arguments
- x
A position in the data object
- Data
A data object
- reps
The number of stochastic samples of the MP recommendation(s)
- plot
Logical. Show the plot?
- yrsmth
Years over which the average index is calculated.
- xx
Parameter controlling the fraction of mean catch to start using in first year
- Imulti
Parameter controlling how much larger target CPUE / index is compared with recent levels.
Value
An object of class Rec-class with the TAC slot populated with a numeric vector of length reps
Details
Four index/CPUE target MPs proposed by Geromont and Butterworth 2014. Tested by Carruthers et al. 2015.
The TAC is calculated as: If \(I_\textrm{recent} \geq I_0\): $$\textrm{TAC}= 0.5 \textrm{TAC}^* \left[1+\left(\frac{I_\textrm{recent} - I_0}{I_\textrm{target} - I_0}\right)\right]$$
else: $$\textrm{TAC}= 0.5 \textrm{TAC}^* \left[\frac{I_\textrm{recent}}{I_0}^2\right]$$
where \(I_0\) is \(0.8 I_{\textrm{ave}}\) (the average index over the 2 x yrsmth years prior to the projection period),
\(I_\textrm{recent}\) is the average index over the past yrsmth years, and
\(I_\textrm{target}\) is Imulti times \(I_{\textrm{ave}}\),
and \(\textrm{TAC}^*\) is:
$$(1-x)C$$
where \(x\) is argument xx and C is the average catch over the last 5 years of the historical period.
Functions
Itarget1(): The less precautionary TAC-based MPItarget2(): Increasing biologically precautionary TAC-based MPItarget3(): Increasing biologically precautionary TAC-based MPItarget4(): The most biologically precautionary TAC-based MP
Rendered Equations
See Online Documentation for correctly rendered equations
References
Carruthers et al. 2015. Performance evaluation of simple management procedures. ICES J. Mar Sci. 73, 464-482.
Geromont, H.F., Butterworth, D.S. 2014. Generic management procedures for data-poor fisheries; forecasting with few data. ICES J. Mar. Sci. 72, 251-261. doi:10.1093/icesjms/fst232
See also
Other Index methods:
GB_slope(),
GB_target(),
Gcontrol(),
ICI(),
Iratio(),
Islope1(),
Itarget1_MPA(),
ItargetE1()
Examples
Itarget1(1, MSEtool::Atlantic_mackerel, plot=TRUE)
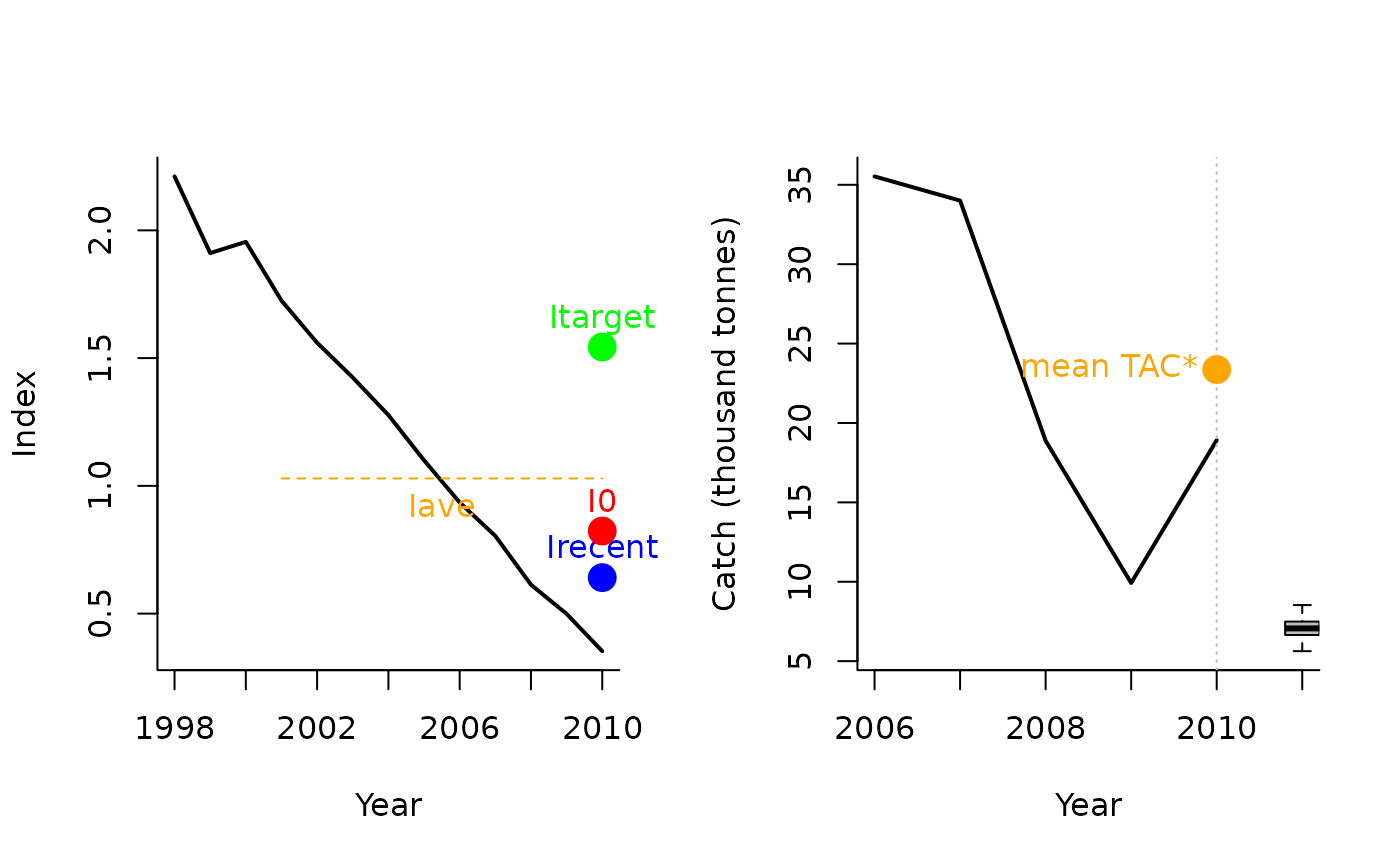 #> TAC (median)
#> 7.025526
Itarget2(1, MSEtool::Atlantic_mackerel, plot=TRUE)
#> TAC (median)
#> 7.025526
Itarget2(1, MSEtool::Atlantic_mackerel, plot=TRUE)
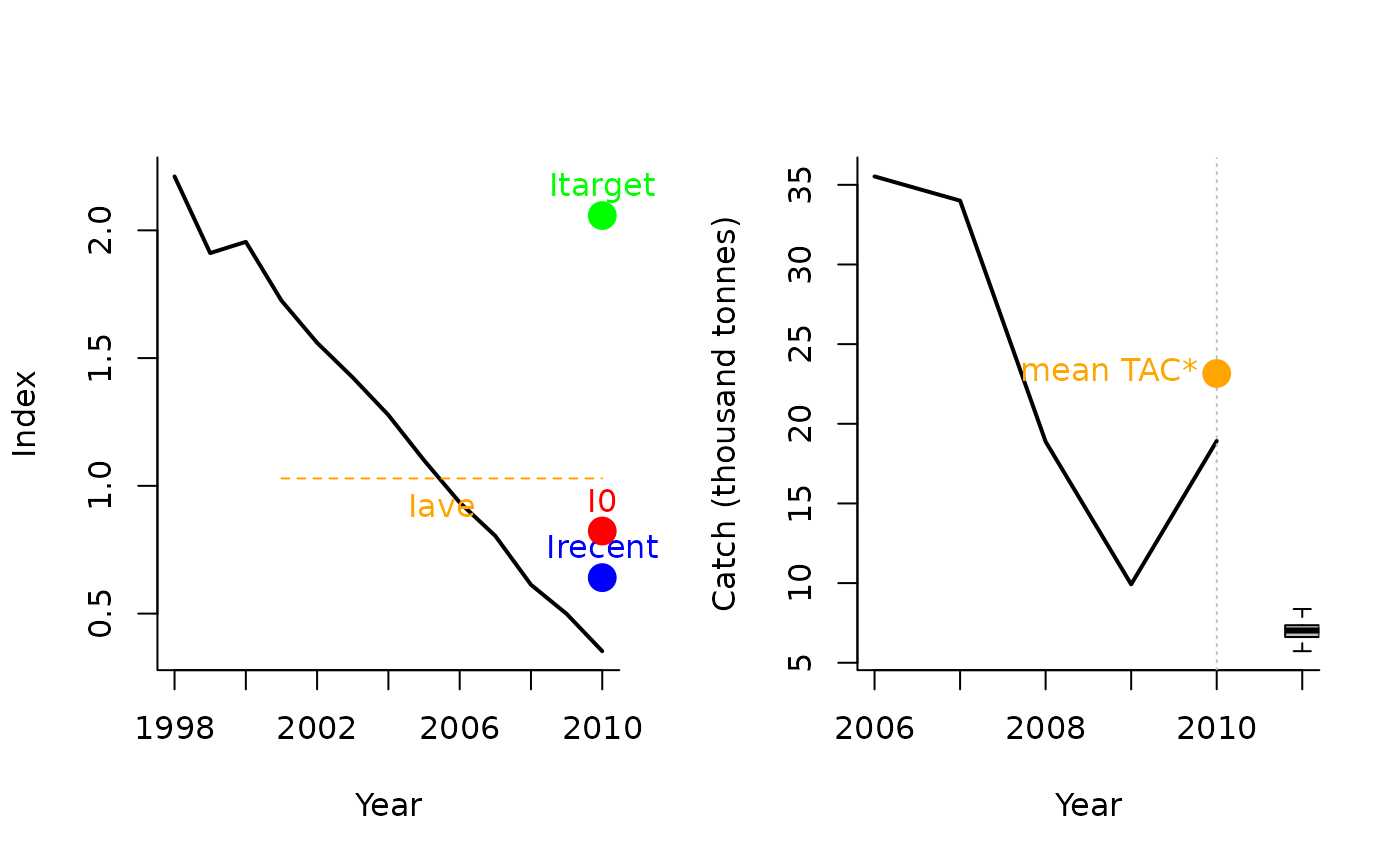 #> TAC (median)
#> 7.02446
Itarget3(1, MSEtool::Atlantic_mackerel, plot=TRUE)
#> TAC (median)
#> 7.02446
Itarget3(1, MSEtool::Atlantic_mackerel, plot=TRUE)
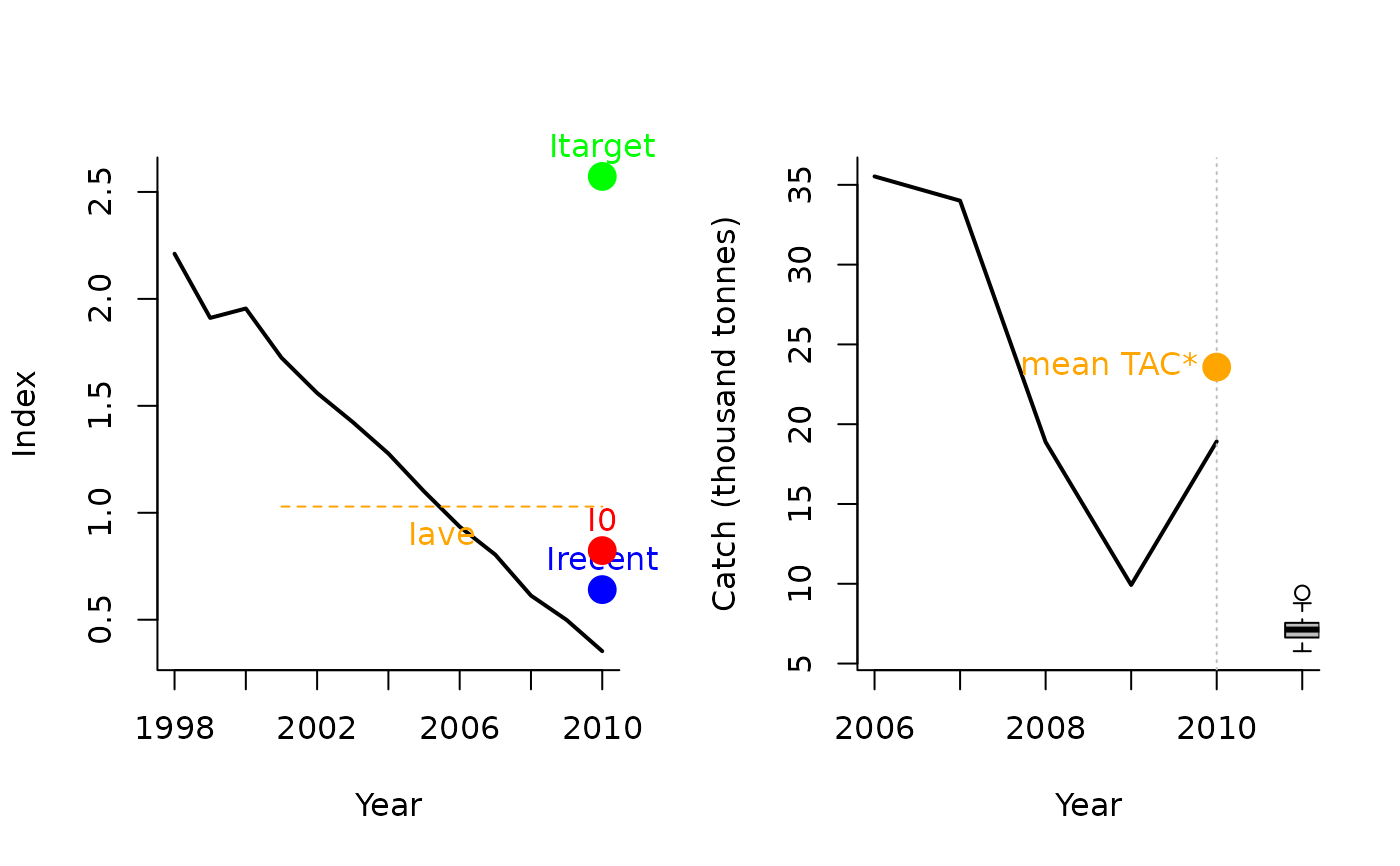 #> TAC (median)
#> 7.158908
Itarget4(1, MSEtool::Atlantic_mackerel, plot=TRUE)
#> TAC (median)
#> 7.158908
Itarget4(1, MSEtool::Atlantic_mackerel, plot=TRUE)
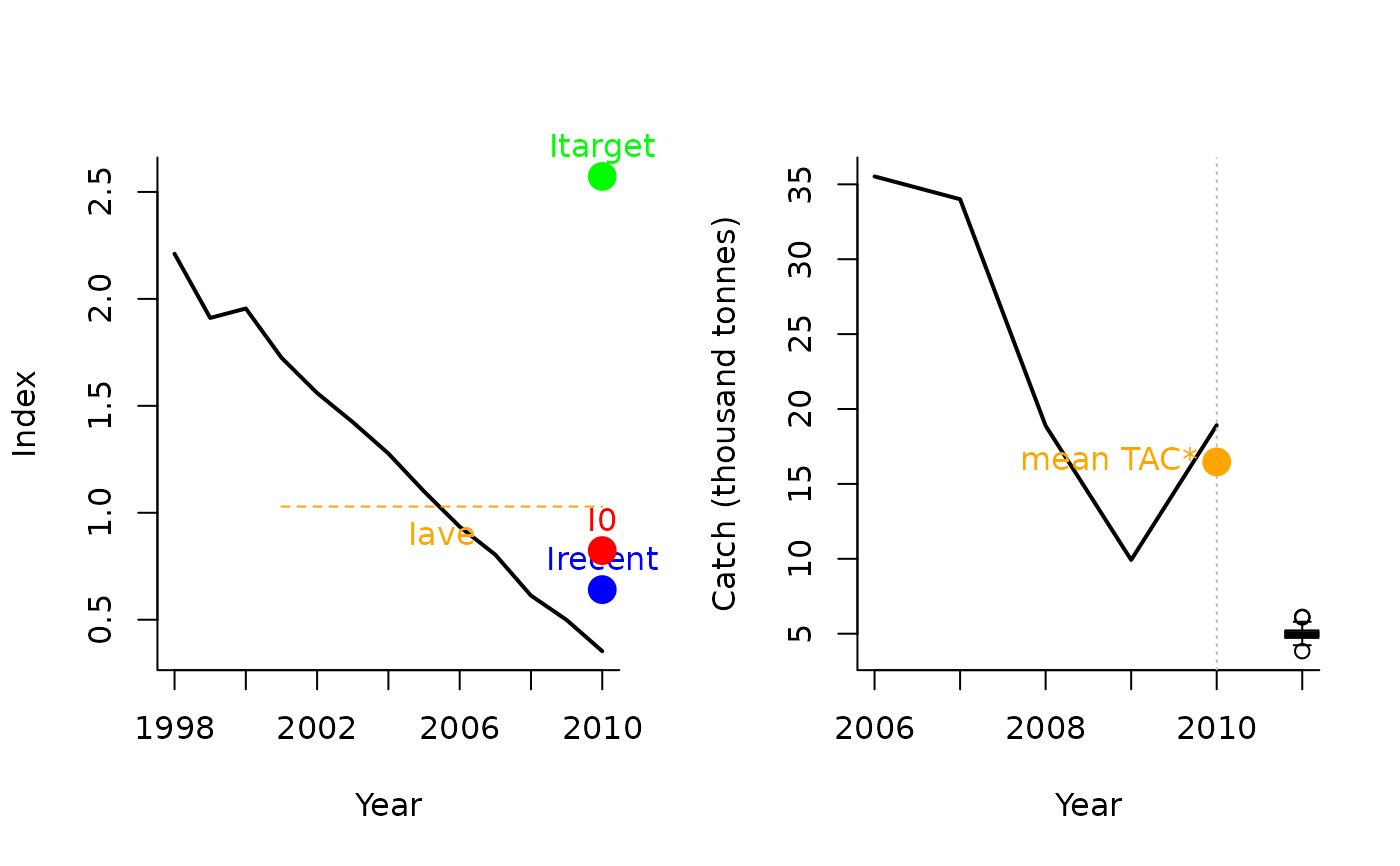 #> TAC (median)
#> 4.950853
#> TAC (median)
#> 4.950853