Skip to contents

Yield Per Recruit analysis to get FMSY proxy F01

YPR.Rd

A simple yield per recruit approximation to FMSY (F01) which is the position of the ascending YPR curve for which dYPR/dF = 0.1(dYPR/d0)

Usage

YPR(x, Data, reps = 100, plot = FALSE)

YPR_CC(x, Data, reps = 100, plot = FALSE, Fmin = 0.005)

YPR_ML(x, Data, reps = 100, plot = FALSE)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

Fmin

The minimum fishing mortality rate inferred from the catch-curve analysis

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC} = F_{0.1} A$$ where \(F_{0.1}\) is the fishing mortality (F) where the slope of the yield-per-recruit (YPR) curve is 10\

The YPR curve is calculated using an equilibrium age-structured model with life-history and selectivity parameters sampled from the Data object.

The variants of the YPR MP differ in the method to estimate current abundance (see Functions section below). #'

Functions

  • YPR: Requires an external estimate of abundance.

  • YPR_CC: A catch-curve analysis is used to determine recent Z which given M (Mort) gives F and thus abundance = Ct/(1-exp(-F))

  • YPR_ML: A mean-length estimate of recent Z is used to infer current abundance.

Note

Based on the code of Meaghan Bryan

Required Data

See Data-class for information on the Data object

YPR: Abun, LFS, MaxAge, vbK, vbLinf, vbt0

YPR_CC: CAA, Cat, LFS, MaxAge, vbK, vbLinf, vbt0

YPR_ML: CAL, Cat, LFS, Lbar, Lc, MaxAge, Mort, vbK, vbLinf, vbt0

Rendered Equations

See Online Documentation for correctly rendered equations

References

Beverton and Holt. 1954.

Author

Meaghan Bryan and Tom Carruthers

Examples

YPR(1, MSEtool::SimulatedData, plot=TRUE)

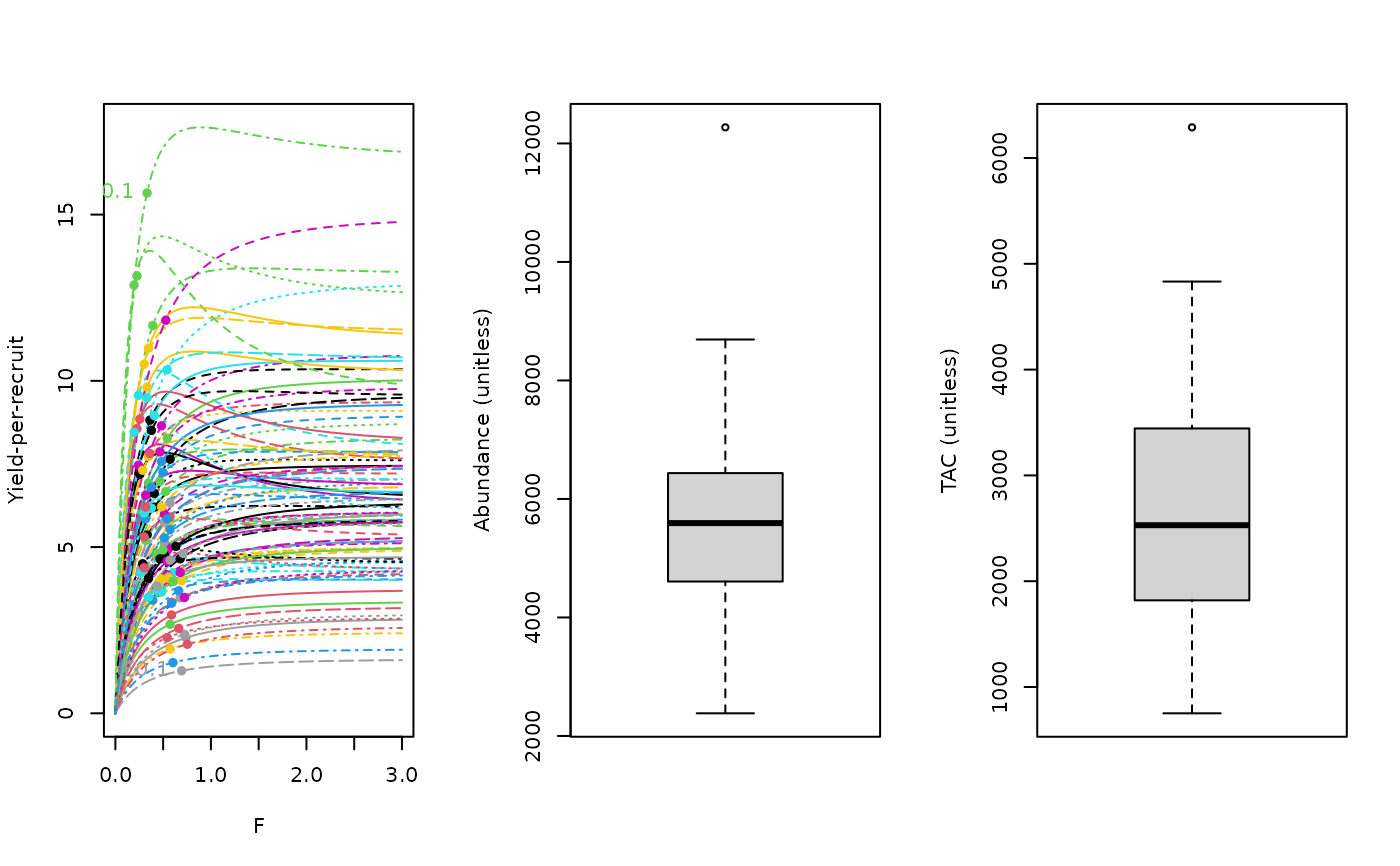#> TAC (median) 
#>     2529.097 
YPR_CC(1, MSEtool::SimulatedData, plot=TRUE)

#> TAC (median) 
#>     3494.597 
YPR_ML(1, MSEtool::SimulatedData, plot=TRUE)

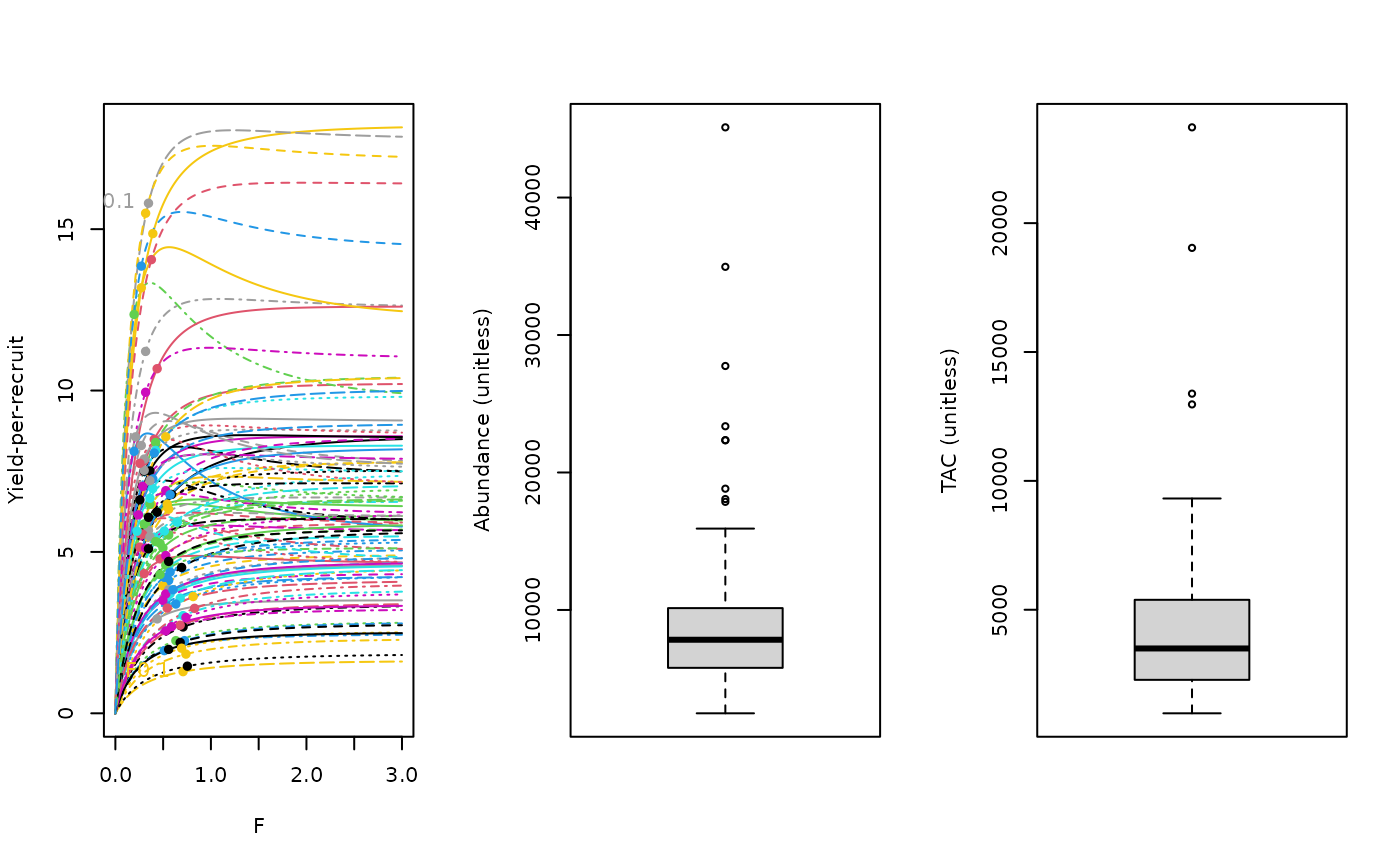#> TAC (median) 
#>     1246.669