SBT simple MP

An MP that makes incremental adjustments to TAC recommendations based on the apparent trend in CPUE, a an MP that makes incremental adjustments to TAC recommendations based on index levels relative to target levels (BMSY/B0) and catch levels relative to target levels (MSY).

Usage

SBT1(
  x,
  Data,
  reps = 100,
  plot = FALSE,
  yrsmth = 10,
  k1 = 1.5,
  k2 = 3,
  gamma = 1
)

SBT2(x, Data, reps = 100, plot = FALSE, epsR = 0.75, tauR = 5, gamma = 1)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

yrsmth

The number of years for evaluating trend in relative abundance indices

k1

Control parameter

k2

Control parameter

gamma

Control parameter

epsR

Control parameter

tauR

Control parameter

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

For SBT1 the TAC is calculated as: $$\textrm{TAC}_y = \left\{\begin{array}{ll} C_{y-1} (1+K_2 \left| \lambda \right| ) & \textrm{if } \lambda \geq 0 \\ C_{y-1} (1-K_1 \left| \lambda \right| ^\gamma) & \textrm{if } \lambda < 0\\ \end{array}\right. $$ where \(\lambda\) is the slope of index over the last yrmsth years, and \(K_1\), \(K_2\), and \(\gamma\) are arguments to the MP.

For SBT2 the TAC is calculated as: $$\textrm{TAC}_y = 0.5 (C_{y-1} + C_\textrm{targ}\delta)$$ where \(C_{y-1}\) is catch in the previous year, \(C_{\textrm{targ}}\) is a target catch (Data@Cref), and : $$\delta= \left\{\begin{array}{ll} R^{1-\textrm{epsR}} & \textrm{if } R \geq 1 \\ R^{1+\textrm{epsR}} & \textrm{if } R < 1 \\ \end{array}\right. $$ where \(\textrm{epsR}\) is a control parameter and: \(R = \frac{\bar{r}}{\phi}\) where \(\bar{r}\) is mean recruitment over last tauR years and \(\phi\) is mean recruitment over last 10 years.

This isn't exactly the same as the proposed methods and is stochastic in this implementation. The method doesn't tend to work too well under many circumstances possibly due to the lack of 'tuning' that occurs in the real SBT assessment environment. You could try asking Rich Hillary at CSIRO about this approach.

Functions

• SBT1: Simple SBT MP

• SBT2: Complex SBT MP

Required Data

See Data-class for information on the Data object

SBT1: Cat, Ind, Year

SBT2: Cat, Cref, Rec

Rendered Equations

See Online Documentation for correctly rendered equations

References

http://www.ccsbt.org/site/recent_assessment.php

Author

T. Carruthers

Examples

SBT1(1, Data=MSEtool::SimulatedData, plot=TRUE)

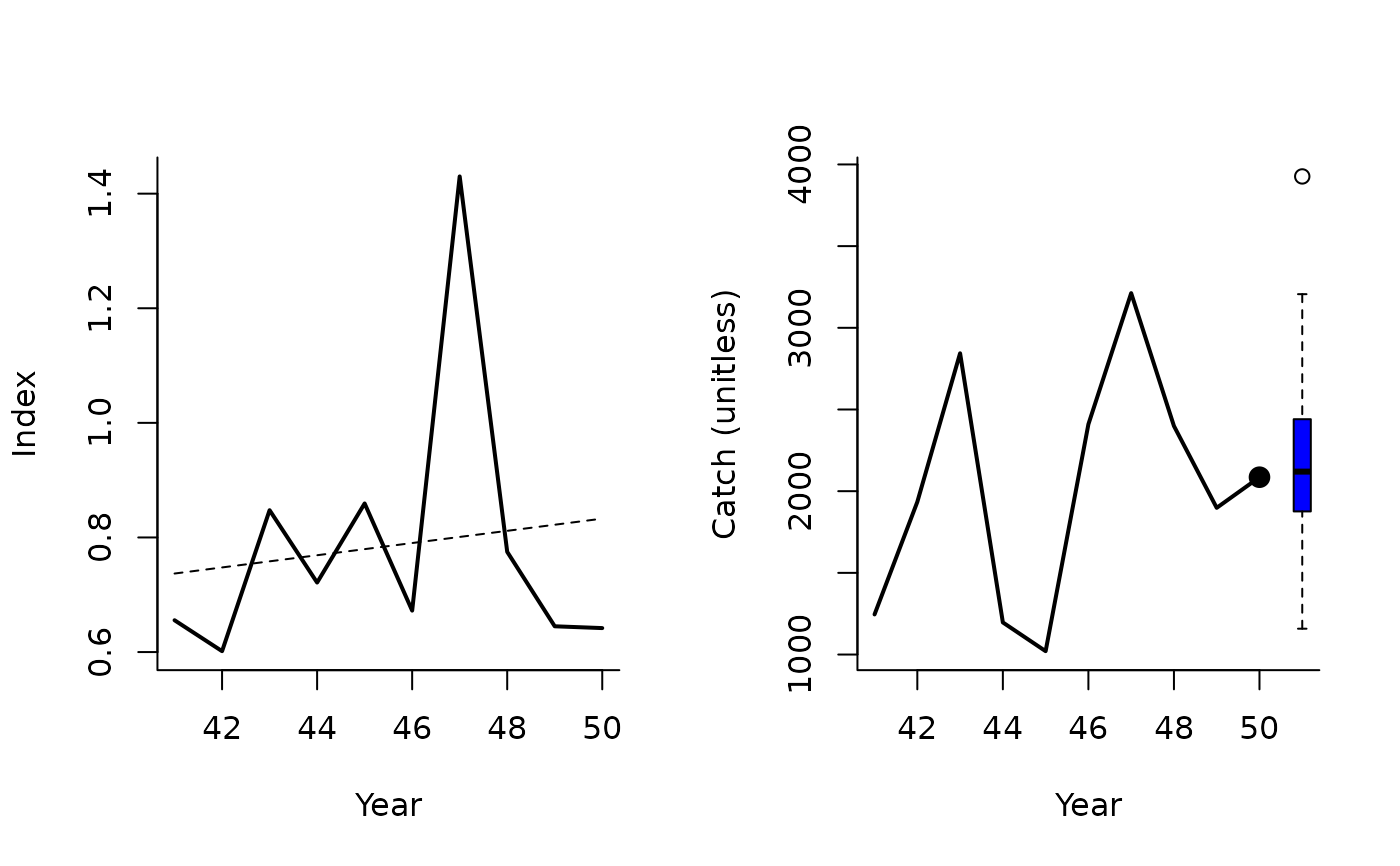#> TAC (median) 
#>     2119.745 
SBT2(1, Data=MSEtool::SimulatedData, plot=TRUE)

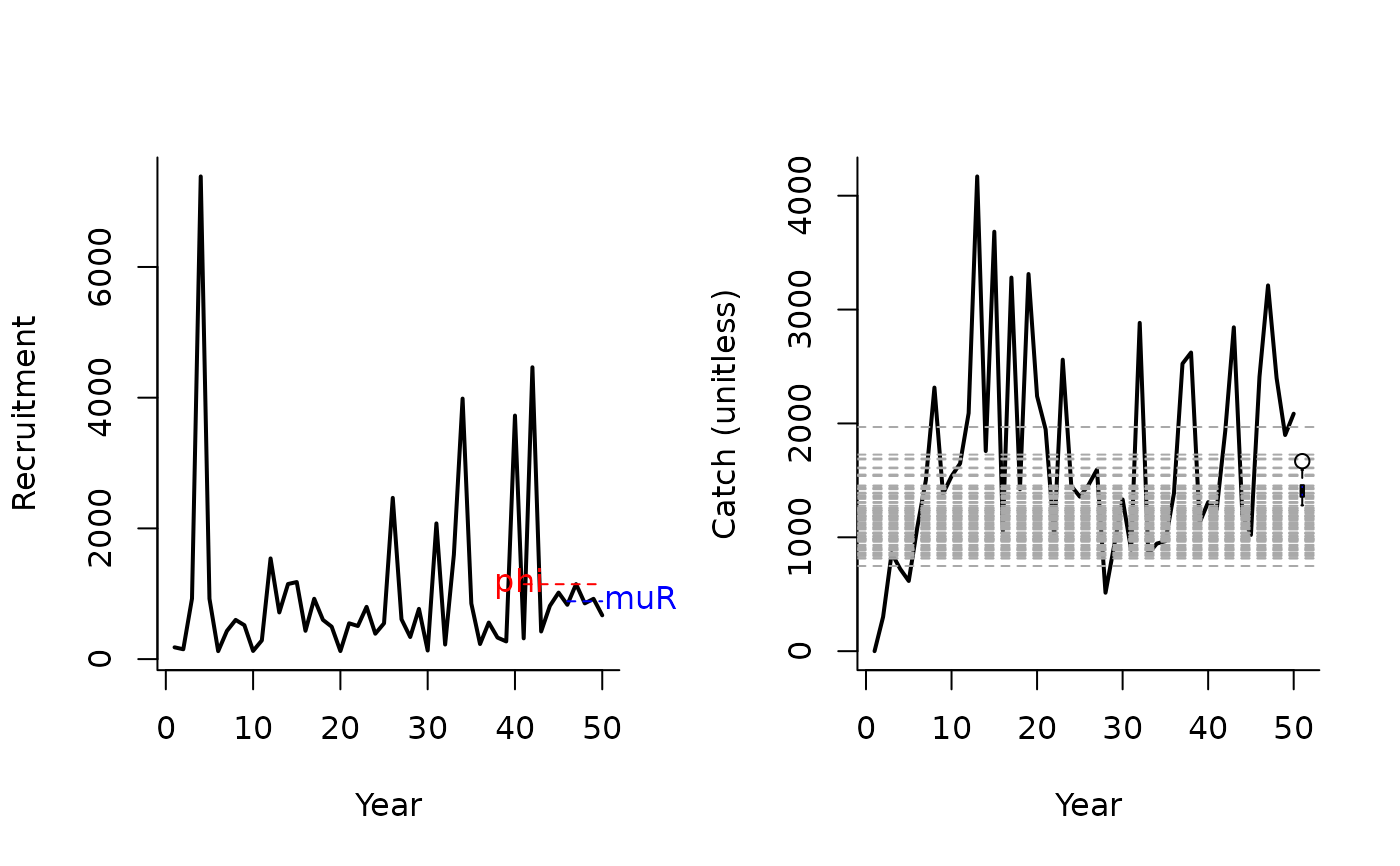#> TAC (median) 
#>      1408.56