Skip to contents

Mean length-based indicator MP of Jardim et al. 2015

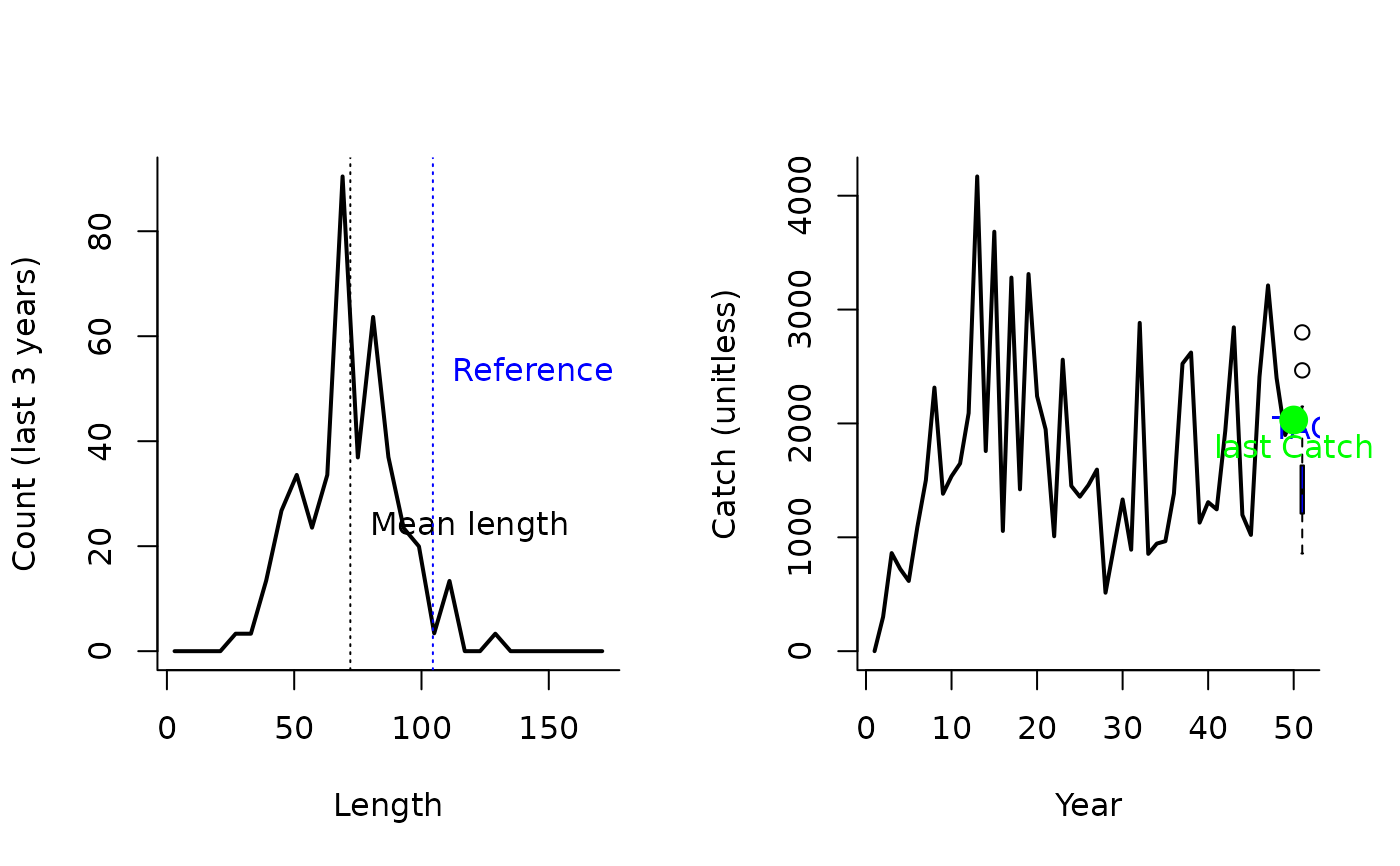
Lratio_BHI.Rd

The TAC is calculated as the most recent catch, modified by the ratio alpha, where the numerator is the mean length of the catch (of lengths larger than Lc) and the denominator is the mean length expected at MSY. Here, Lc is the length at full selection (LFS).

Usage

Lratio_BHI(x, Data, reps = 100, plot = FALSE, yrsmth = 3)

Lratio_BHI2(x, Data, reps = 100, plot = FALSE, yrsmth = 3)

Lratio_BHI3(x, Data, reps = 100, plot = FALSE, yrsmth = 3)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

yrsmth

The most recent years of data to smooth the calculation of the mean length

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

The TAC is calculated as: $$\textrm{TAC}_y = C_{y-1} \frac{L}{L_\textrm{ref}}$$ where \(C_{y-1}\) is the catch from the previous year, \(L\) is the mean length of the catch over the last yrsmth years (of lengths larger than Lc) and \(L_\textrm{ref}\) is the mean length expected at MSY. Here, Lc is the length at full selection (LFS).

Functions

  • Lratio_BHI(): Assumes M/K = 1.5 and FMSY/M = 1. Natural mortality M and von Bertalanffy K are not used in this MP (see Appendix A of Jardim et al. 2015).

  • Lratio_BHI2(): More general version that calculates the reference mean length as a function of M, K, and presumed FMSY/M.

  • Lratio_BHI3(): A modified version of Lratio_BHI2 where mean length is calculated for lengths > modal length (Lc)

Required Data

See Data-class for information on the Data object

Lratio_BHI: CAL, CAL_bins, Cat, LFS, vbLinf

Lratio_BHI2: CAL, CAL_bins, Cat, FMSY_M, LFS, Mort, vbK, vbLinf

Lratio_BHI3: CAL, CAL_bins, Cat, FMSY_M, LFS, Mort, vbK, vbLinf

Rendered Equations

See Online Documentation for correctly rendered equations

References

Ernesto Jardim, Manuela Azevedo, Nuno M. Brites, Harvest control rules for data limited stocks using length-based reference points and survey biomass indices, Fisheries Research, Volume 171, November 2015, Pages 12-19, ISSN 0165-7836, https://doi.org/10.1016/j.fishres.2014.11.013

See also

Other Length target MPs: Ltarget1(), LtargetE1()

Author

Coded by Q. Huynh. Developed by Jardim et al. (2015)

Examples

Lratio_BHI(1, Data=MSEtool::SimulatedData, plot=TRUE)

#> TAC (median) 
#>     1404.026 

Lratio_BHI2(1, Data=MSEtool::SimulatedData, plot=TRUE)

#> TAC (median) 
#>     1464.231 

Lratio_BHI3(1, Data=MSEtool::SimulatedData, plot=TRUE)

#> TAC (median) 
#>     2154.358