Skip to contents

FMSY/M ratio methods

Fratio.Rd

Calculates the OFL based on a fixed ratio of FMSY to M multiplied by a current estimate of abundance.

Usage

Fratio(x, Data, reps = 100, plot = FALSE)

Fratio4010(x, Data, reps = 100, plot = FALSE)

DepF(x, Data, reps = 100, plot = FALSE)

Fratio_CC(x, Data, reps = 100, plot = FALSE, Fmin = 0.005)

Fratio_ML(x, Data, reps = 100, plot = FALSE)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

Fmin

Minimum current fishing mortality rate for the catch-curve analysis

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

A simple method that tends to outperform many other approaches alarmingly often even when current biomass is relatively poorly known. The low stock crash potential is largely due to the quite large difference between Fmax and FMSY for most stocks.

The TAC is calculated as: $$\textrm{TAC} = F_{\textrm{MSY}} A$$ where \(F_{\textrm{MSY}}\) is calculated as \(\frac{F_\textrm{MSY}}{M} M\) and A is estimate of current abundance.

The MP variants differ in the assumption of current abundance (see Functions section below)

Functions

  • Fratio: Requires an estimate of current abundance (i.e Data@Abun)

  • Fratio4010: Paired with the 40-10 rule that throttles back the OFL to zero at 10 percent of unfished biomass. Requires an estimate of current depletion.

  • DepF: Depletion Corrected Fratio: the Fratio MP with a harvest control rule that reduces F according to the production curve given an estimate of current stock depletion (made-up for this package).

  • Fratio_CC: Current abundance is estimated using average catch and estimate of F from an age-based catch curve

  • Fratio_ML: Current abundance is estimated using average catch and estimate of F from mean lengths

Required Data

See Data-class for information on the Data object

Fratio: Abun, FMSY_M, Mort

Fratio4010: Abun, Dep, FMSY_M, Mort

DepF: Abun, Dep, FMSY_M, Mort

Fratio_CC: CAA, Cat, FMSY_M, Mort

Fratio_ML: CAL, Cat, FMSY_M, Lbar, Lc, Mort, vbK, vbLinf

Rendered Equations

See Online Documentation for correctly rendered equations

References

Gulland, J.A., 1971. The fish resources of the ocean. Fishing News Books, West Byfleet, UK.

Martell, S., Froese, R., 2012. A simple method for estimating MSY from catch and resilience. Fish Fish. doi: 10.1111/j.1467-2979.2012.00485.x.

See also

Other Fmsy/M methods: DynF(), Fadapt()

Author

T. Carruthers

Examples

Fratio(1, MSEtool::Atlantic_mackerel, plot=TRUE)

#> TAC (median) 
#>     3.668003 
Fratio4010(1, MSEtool::Atlantic_mackerel, plot=TRUE)

#> TAC (median) 
#>     2.332493 
Fratio_CC(1, MSEtool::SimulatedData, plot=TRUE)

#> TAC (median) 
#>     2249.549 
Fratio_ML(1, MSEtool::SimulatedData, plot=TRUE)

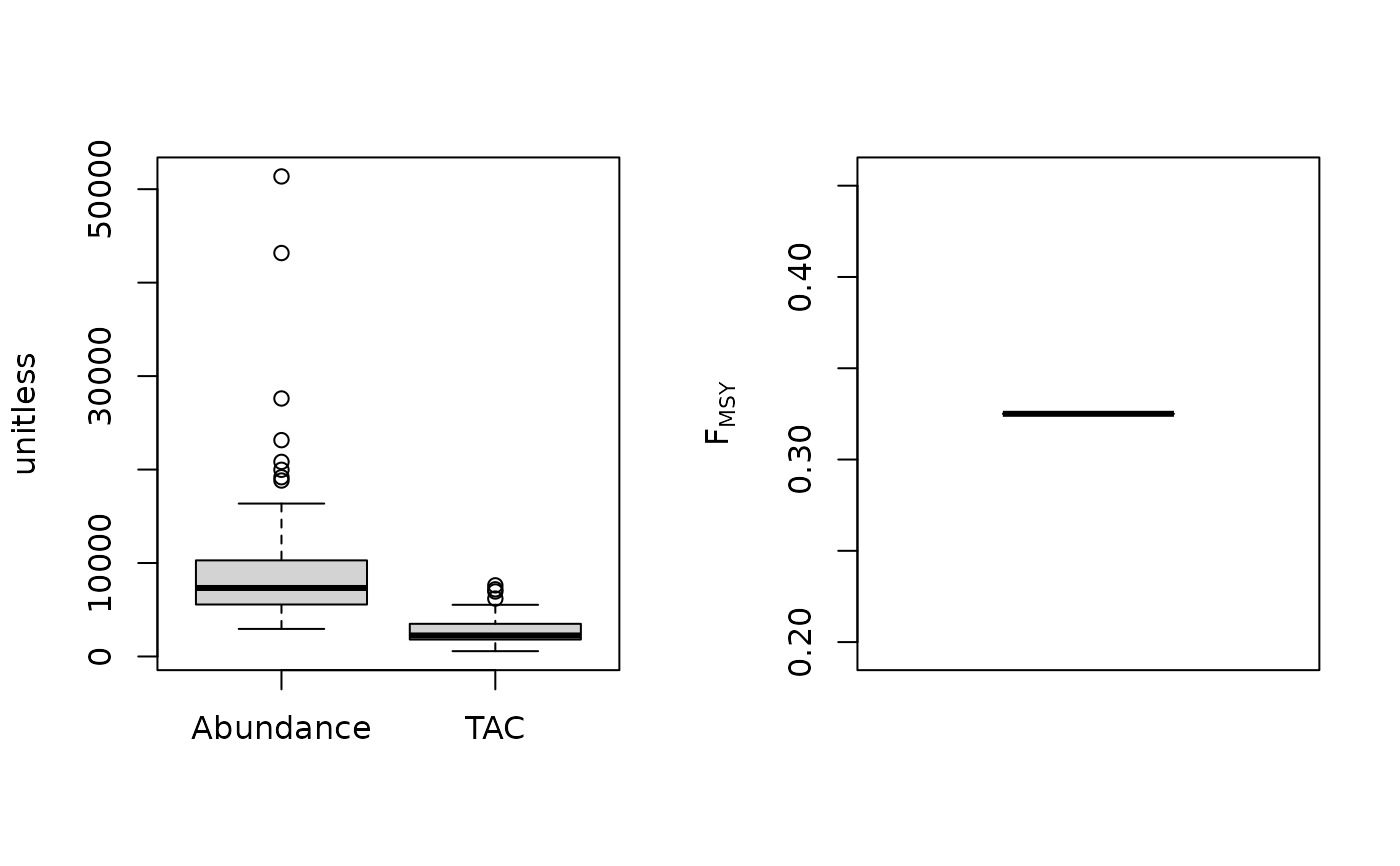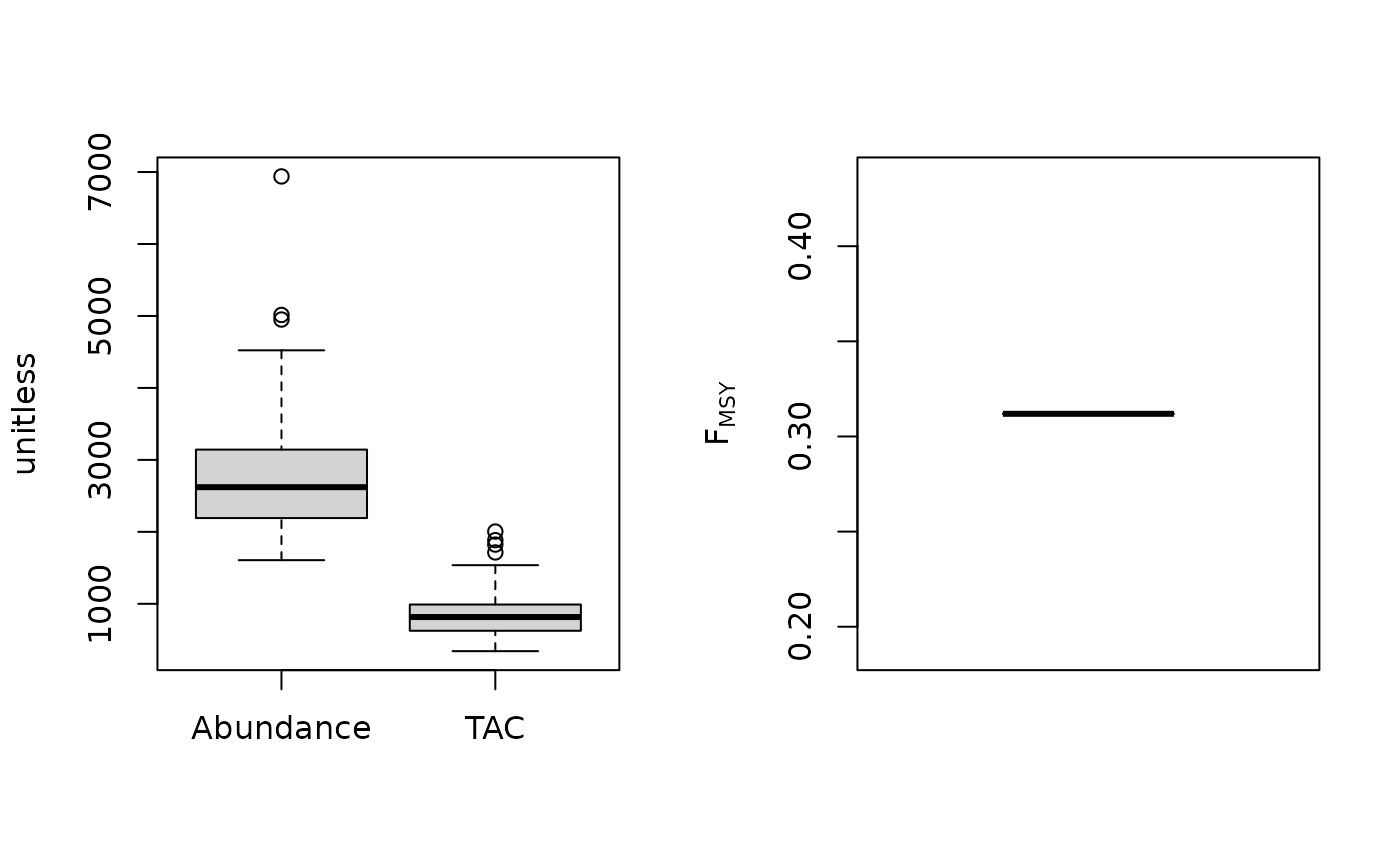#> TAC (median) 
#>     816.1283