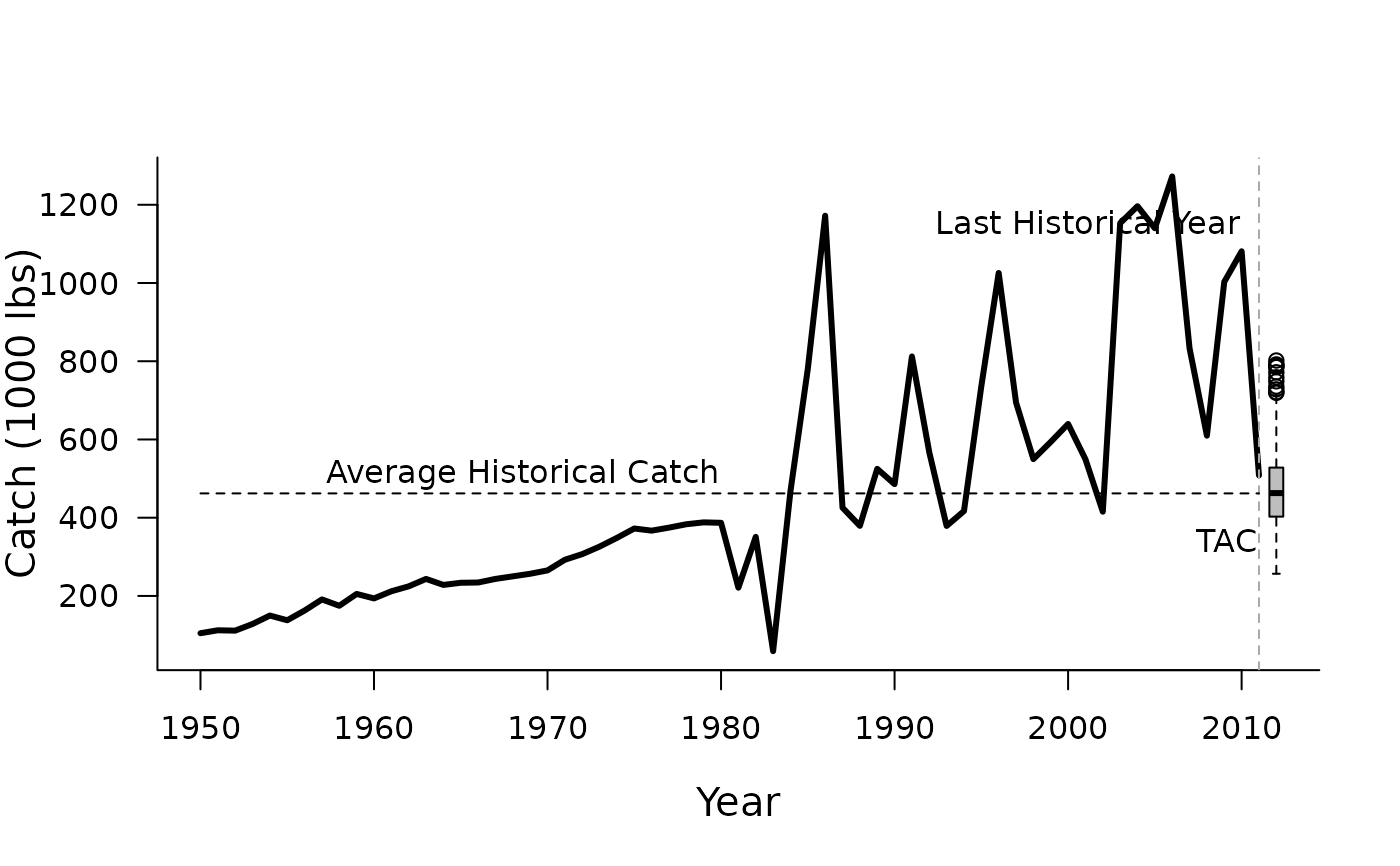
Average Catch

A simple average catch MP that is included to demonstrate a 'status quo' management option

Usage

AvC(x, Data, reps = 100, plot = FALSE)

Arguments

x

A position in the data object

Data

A data object

reps

The number of stochastic samples of the MP recommendation(s)

plot

Logical. Show the plot?

Value

An object of class Rec-class with the TAC slot populated with a numeric vector of length reps

Details

The average catch method is very simple. The mean historical catch is calculated and used to set a constant catch limit (TAC). If reps > 1 then the reps samples are drawn from a log-normal distribution with mean TAC and standard deviation (in log-space) of 0.2.

For completeness, the TAC is calculated by:

$$\textrm{TAC} =\frac{\sum_{y=1}^{\textrm{n}}{C_y}}{\textrm{n}}$$

where \(\textrm{TAC}\) is the the mean catch recommendation, \(n\) is the number of historical years, and \(C_y\) is the catch in historical year \(y\)

Required Data

See Data-class for information on the Data object

AvC: Cat, LHYear, Year

Rendered Equations

See Online Documentation for correctly rendered equations

See also

Other Average Catch MPs: AvC_MLL(), DCACs()

Author

T. Carruthers

Examples

Rec <- AvC(1, MSEtool::Cobia, reps=1000, plot=TRUE) # 1,000 log-normal samples with CV = 0.2